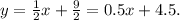Question

Use the point-slope formula to write an equation of the line that passes through (- 1, 4) and (1, 5 ) .Write the answer in slope-intercept form (if possible).The equation of the line is Hi everyone, this is very hard for me I have tried 18 times by myself before I found you folks .I need this in the simplest terms as i don't get it if it is too involved .

Answer 1

To solve this problem, we will compute the slope of the line and then we will use it to find the equation of the line.

To determine the slope of a line that passes through points (x₁,y₁), and (x₂,y₂), we can use the following formula:

`m=(y_2-y_1)/(x_2-x_1).`

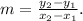
Substituting

`\begin{gathered} (x_2,y_2)=(-1,4), \\ (x_1,y_1)=(1,5), \end{gathered}`

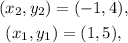
in the above formula, we get:

`s=(4-5)/(-1-1)=(-1)/(-2)=(1)/(2).`

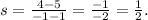
Now, with the above slope, we use the following formula for the equation of a line with slope m:

`y-y_1=m(x-x_1).`

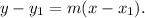
Finally, we substitute one of the points:

`y-5=(1)/(2)(x-1)`

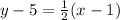
and take the equation to its slope-intercept form:

`\begin{gathered} y-5=(1)/(2)(x-1), \\ y-5=(1)/(2)x-(1)/(2), \\ y=(1)/(2)x+(9)/(2). \end{gathered}`

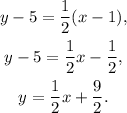
Answer:

`y=(1)/(2)x+(9)/(2)=0.5x+4.5.`