We can calculate the rate of change as the slope between two points, like (1,2) and (2,4).
The slope is:
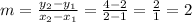
If this is a linear function, this slope m has to be constant.
We will calculate the slope between other points, like (3,8) and (4,16):
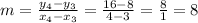
The slope is not constant, so this function is not a linear function.
If we look at how f(x) increases, we can prove that f(x) is:
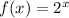
and this function is an exponential function.
Answer: Option B (exponential function).