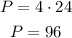Question

Find the area and the perimeter of the following rhombus. round to the nearest whole number if needed.

Answer 1

`\begin{gathered} A=572 \\ P=96 \end{gathered}`

Step-by-step explanation

To find the area of the rhombus, we have to first find the length of the other diagonal.

We are given half one diagonal and the side length.

They form a right angle triangle with half the other diagonal. That is:

We can find x using Pythagoras theorem:

`\begin{gathered} 24^2=x^2+16^2 \\ x^2=24^2-16^2=576-256 \\ x^2=320 \\ x=\sqrt[]{320} \\ x=17.89 \end{gathered}`

This means that the length of the two diagonals is:

`\begin{gathered} \Rightarrow2\cdot16=32 \\ \Rightarrow2\cdot17.89=35.78 \end{gathered}`

The area of a rhombus is given as:

`A=(p\cdot q)/(2)`

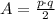
where p and q are the lengths of the diagonal.

Therefore, the area of the rhombus is:

`\begin{gathered} A=(32\cdot35.78)/(2) \\ A=572.48\approx572 \end{gathered}`

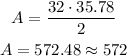
The perimeter of a rhombus is given as:

`P=4L`

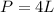
where L = length of side of the rhombus

Therefore, the perimeter of the rhombus is:

`\begin{gathered} P=4\cdot24 \\ P=96 \end{gathered}`