Question

Let g(x) be the transformation, vertical translation 5 units down, of f(x)= 3x+9. Write the rule for g(x).

Answer 1

We can see the next function:

`f(x)=3x+9`

And we need to translate this function 5 units down, which results in the function g(x).

To find the rule for g(x), we can follow the next steps:

1. We know that the general rule for a function translated k units down is given by:

`f(x)-k\rightarrow\text{ f\lparen x\rparen has been translated by k units down \lparen where k > 0\rparen.}`

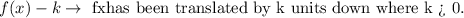
2. Then if we translate the original function by 5 units down, we will have that:

`\begin{gathered} f(x)=3x+9 \\ \\ \\ f(x)-5=3x+9-5\rightarrow g(x) \\ \\ \end{gathered}`

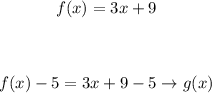
3. Therefore, g(x) will be:

`\begin{gathered} g(x)=3x+9-5=3x+4 \\ \\ g(x)=3x+4 \end{gathered}`

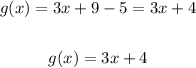
Hence, in summary, we have that the rule for g(x) is g(x) = 3x + 4 (option A).