Question

The following table represents C, an appliance repairman’s charges based on t, the hours it takes to make a repair.Which of the following equations could be used to determine the repairman’s charges for a repair?A: C=27t +3B: C=27tC: C=35tD: C=35t + 2

Answer 1

Given the table below

To find the equation of the values of the table, we will first calculate the rate of change, then use a point and the rate of change calculated fo find the equation for the repairman's charges for the repair

To find the rate of change we have

`\text{ Point 1}\Rightarrow(1,62)\Rightarrow t_1=1,c_1=62`
`\text{ Point 2}\Rightarrow(3,116)\Rightarrow t_2=3,c_2=116`

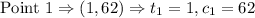
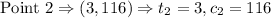
The rate of change formula is

`m=(c_2-c_1)/(t_2-t_1)=(116-62)/(3-1)=(54)/(2)=27`

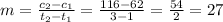
Having calculated the rate, we can use slope and one point form equation of a line to get the desired equation. This is given below:

`c-c_1=m(t-t_1)`

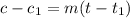
Substitute the given values of t and c and the rate in the formula above

`\begin{gathered} c-62=27(t-1) \\ c-62=27t-27 \\ c=27t-27+62 \\ c=27t+35 \end{gathered}`

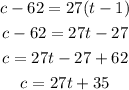
Hence, the repairman's charges for a repair is given as C = 27t + 35