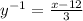Question

What is the inverse of the given relation?y = 3x + 12I need to understand the step by step breakdown for how to solve this problem.

Answer 1

Given the function y, we want to find the inverse function y^-1.

Then, replace every x with a y and every y with an x. It yields,

`x=3y+12`

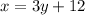
now, solve the equation for y. So, by subtracting 12 to both sides, we have

`x-12=3y`

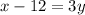
or equivalently,

`3y=x-12`

and, by dividing both sides by 3, we obtain

`y=(x-12)/(3)`

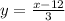
Finally, replace y with y^-1. Then, the inverse function is given by:

`y^(-1)=(x-12)/(3)`