Given that the pipe has varying cross-sections.
The diameter of one section is d1 = 9.1 cm and the diameter of second section is d2 = 12.6 cm.
Also, the fluid has the density,
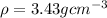
The area of the cross-section for the first section is
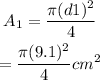
The area of the cross-section for the second section is

The flow speed for the first section is v1 = 339 cm s^-1
The flow speed for the second section will be v2.
(a) The flow speed for the second section can be calculated as
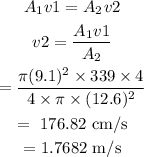
(b) The pressure for first section is p1 = 2.93 x 10^5 Pa
The pressure for the second section will be p2.
The pressure for the second section can be calculated by the formula,
