Question

Find the average rate of change of the following equation on the given interval. y=3x+1 on [45,48]

Answer 1

Given:

The equation is given as,

`y=3x+1`

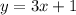
The interval is given as,

`\lbrack a,b\rbrack=\lbrack45,48\rbrack`

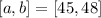
The objective is to find the average rate of change.

Step-by-step explanation:

The general formula to find the average rate of change is,

`A=(f(b)-f(a))/(b-a)\text{ . . . . (1)}`

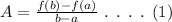
On plugging the function in the equation (1),

`A=((3(48)+1)-(3(45)+1))/(48-45)`

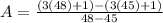
On further solving the above equation,

`\begin{gathered} A=(145-136)/(3) \\ =(9)/(3) \\ =3 \end{gathered}`

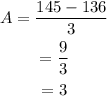
Hence, the average rate of change is 3.