We have to solve for c:
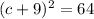
When we have quadratic expressions, we have to take into account that each number has two possible square roots: one positive and one negative.
We can see it in this example: the square root of 4 can be 2 or -2. This is beacuse both (-2)² and 2² are equal to 4.
Then, taking that into account, we can solve this expression as:
![\begin{gathered} (c+9)^2=64 \\ c+9=\pm\sqrt[]{64} \\ c+9=\pm8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/s6n5tdr7isgodhmrqzintd9lphda830kee.png)
We then calculate the first solution for the negative value -8:
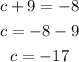
And the second solution for the positive value 8:
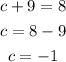
Then, the two solutions are c = -17 and c = -1.
We can check them replacing c with the corresponding values we have found:
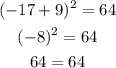
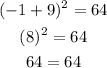
Both solutions check the equality, so they are valid solutions.
Answer: -17 and -1.