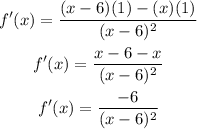ANSWER

Step-by-step explanation
We want to find the derivative of the function:
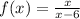
The quotient rule states that:
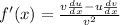
where u = the numerator of the function
v = the denominator of the function
From the function, we have that:
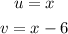
Now, we have to differentiate both u and v:
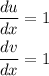
Therefore, the derivative of the function is: