Given: The angles as shown in the image
![\begin{gathered} m\angle DEY=105^0 \\ m\angle DEF=27x+3 \\ m\angle YEF=6x+3 \end{gathered}]()
To Determine: The measure of angle DEF
Solution
It can be observed that
![\begin{gathered} m\angle DEY+m\angle YEF=m\angle DEF \\ Therefore \end{gathered}]()
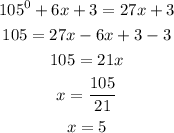
![\begin{gathered} m\angle DEF=21x+3 \\ =21(5)+3 \\ =105+3 \\ =108 \end{gathered}]()
Question 12
Given:
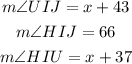
To Determine: The measure of angle HIU
Solution:
It can be observed that
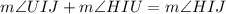
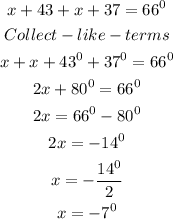
Therefore, the measure of angle HIU would be
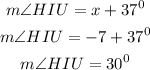
Hence, the measure of angle HIU is 30⁰