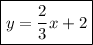Explanation:
Step 1. We are given the graph of a line and we need to find the equation of the line parallel to it that has an x-intercept of -3.
Since the new line will be a parallel line it means that it will have the same slope. Therefore, our first step is to find the slope of the current line.
Given any line, we find the slope as shown in the following example diagram:
Step 2. Using the previous method, the slope of our line is:
The new line will have the same slope of 2/3.
Step 3. We are also told that the x-intercept of the new line is -3, which means that the new line will cross the y-axis at x=-3, that point is:
(-3,0)
We will label that point of our new line as (x1,y1):
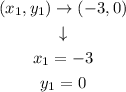
Step 4. So far, we know that the new line will have a slope of 2/3:
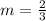
And that it includes the point (-3,0) where x1=-3 and y1=0.
To find the equation, we use the point-slope equation:

Step 5. Substituting the known values into the formula:
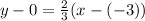
Solving the operations:
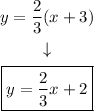
Answer: