Let's call the event of the red die to show a six as event A, and the event of the green die to show a six as event B.
The theoretical probability is defined as the ratio of the number of favourable outcomes to the number of possible outcomes. On both dices, we have 6 possible outcomes(the numbers from 1 to 6), with one favourable outcome(the number 6), therefore, the probabilities of those events are:
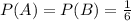
Each roll is independent from each other, then, the probability of both events happening simultaneously is given by their product:
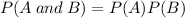
Using the additive rule of probability, we have the following equation for our problem:

the probability that the red die shows a six or the green die shows a six is 11/36.