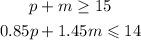Given:
Minimum number of pencils or markers = 15
Maximum amount to spend on pencils and markers = $14
Cost of a pencil = $0.85
Cost of a marker = $1.45
Required: System of inequalities models the situation
Step-by-step explanation:
Let p denote the number of pencil and m be the number of markers
Since the minimum number of pencils or markers is 15, it gives the inequality
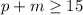
Since the maximum amount to spend on pencils and markers is $14, it gives the inequality
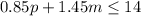
Final Answer: