Question

Identify the explicit formula for the sequence given by the following recursive formula: A) f(n) = –2 + 4(n – 1)B) f(n) = –4 + 2(n – 1)C) f(n) = 4 – 2(n – 1)D) f(n) = 2 – 4(n – 1)

Answer 1

Given the recurssive formula;

`f(n)=\begin{cases}f(1)=-2 \\ f(n)=f(n-1)+4\text{ if n>1}\end{cases}`

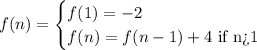
Let's find the sequence using the recurssive formula, we have;

`\begin{gathered} f(2)=f(2-1)+4 \\ f(2)=f(1)+4 \\ f(2)=-2+4 \\ f(2)=2 \\ f(3)=f(3-1)+4 \\ f(3)=f(2)+4 \\ f(3)=2+4 \\ f(3)=6 \\ f(4)=f(4-1)+4 \\ f(4)=f(3)+4 \\ f(4)=6+4 \\ f(4)=10 \end{gathered}`

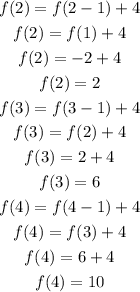
Thus, we have the sequence as;

`-2,2,6,10,\ldots`

We observed that the sequence is an arithmetic sequence with a common difference of 4 and first term of -2.

So, the recursive formula is;

`\begin{gathered} f(n)=f(1)+d(n-1)_{} \\ f(n)=-2+4(n-1) \\ f(n)=-2+4n-4_{} \\ f(n)=4n-6 \end{gathered}`

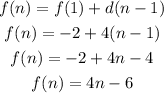
CORRECT OPTION: A