1 Answer

Marc Rochkind · Answer 1 · 2023-11-22T07:00:29+0000

Given:

The point (0,0) lies on the graph f(x) and (4,-3) lies on the graph h(x).

To find:

We need to find the equation for the function h(x).

Step-by-step explanation:

Consider the translation point which is translated horizontally a unit and vertically as b units.

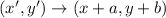
$(x^(\prime),y^(\prime))\rightarrow(x+a,y+b)$

The point (4,-3) can be written as follows.

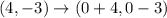
$(4,-3)\rightarrow(0+4,0-3)$

We get the function h(x) after f(x) translated horizontally 4 units right and vertically 3 units down.

The function can be written as follows.

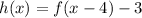
$\text{Replace x=x-4 in f(x)=}\sqrt[]{x\text{ }}\text{ and substitute in the equation.}$

$h(x)=\sqrt[]{x-4}-3$

Final answer:

$h(x)=\sqrt[]{x-4}-3$

Please log in or register to add a comment.