Question

The length of a rectangle is 9 inches more than the width. The perimeter is 34 inches. Find the length I need both length and the width of the rectangle

Answer 1

Step-by-step explanation

The perimeter is the sum of the side lengths of a polygon. Now, let it be:

• l,: the length of the rectangle

,

• w,: the width of the rectangle

Considering the information given and the previous definition, we can write and solve the following system of equations.

`\begin{cases}l=9+w\Rightarrow\text{ Equation 1} \\ l+w+l+w=34\Rightarrow\text{ Equation 2}\end{cases}`

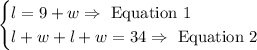
We can use the substitution method to solve the system of equations.

Step 1: We combine like terms in Equation 2.

`\begin{cases}l=9+w\Rightarrow\text{ Equation 1} \\ 2l+2w=34\Rightarrow\text{ Equation 2}\end{cases}`

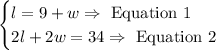
Step 2: We substitute the value of l from Equation 1 into Equation 2.

`\begin{gathered} 2l+2w=34 \\ 2(9+w)+2w=34 \end{gathered}`

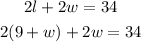
Step 3: We solve for w the resulting equation.

`\begin{gathered} \text{ Apply the distributive property on the left side} \\ 2\cdot9+2\cdot w+2w=34 \\ 18+2w+2w=34 \\ \text{ Add similar terms} \\ 18+4w=34 \\ \text{ Subtract 18 from both sides} \\ 18+4w-18=34-18 \\ 4w=16 \\ \text{ Divide by 4 from both sides} \\ (4w)/(4)=(16)/(4) \\ w=4 \end{gathered}`

Step 4: We replace the value of w in Equation 1.

`\begin{gathered} \begin{equation*} l=9+w \end{equation*} \\ l=9+4 \\ l=13 \end{gathered}`

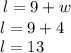
Thus, the solution of the system of equations is:

`\begin{gathered} l=13 \\ w=4 \end{gathered}`Answer

The length of the rectangle is 13 inches, and the width of the rectangle is 4 inches.