Question

A rectangular parking lot has length that is 3 yards less than twice its width. If the area of the land is 299 square yards, what are the dimensions of the land?The parking lot has a width of square yards.

Answer 1

• Width = 13 yards

,

• Length = 23 yards

Explanation:

Let the width of the parking lot = w yards.

The length is 3 yards less than twice its width.

`\implies\text{Length}=(2w-3)\text{ yards}`

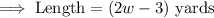
The area of the land = 299 square yards.

`w(2w-3)=299`

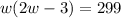
We then solve the equation above for w.

`\begin{gathered} 2w^2-3w=299 \\ \implies2w^2-3w-299=0 \end{gathered}`

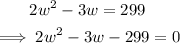
Factor the resulting quadratic expression.

`\begin{gathered} 2w^2-26w+23w-299=0 \\ 2w(w-13)+23(w-13)=0 \\ (2w+23)(w-13)=0 \end{gathered}`

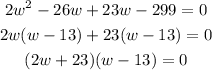
Solve for w.

`\begin{gathered} 2w+23=0\text{ or }w-13=0 \\ 2w=-23\text{ or }w=13 \\ w\\eq-(23)/(2),w=13 \end{gathered}`

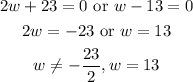
Since w cannot be negative, the parking lot has a width of 13 yards.

Finally, find the length of the parking lot.

`\begin{gathered} 13l=299 \\ l=(299)/(13)=23\text{ yards} \end{gathered}`

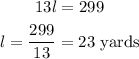
The length of the parking lot is 23 yards.