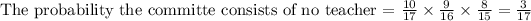Step 1
State the expression for the probability of an event
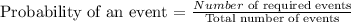
Total number of events = 7+6+4 = 17
Step 2
Find the probability for selection of 3 teachers
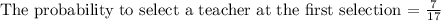
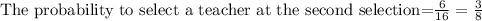
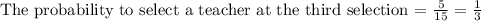
Therefore
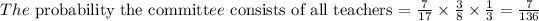
Step 3
Find the probability the committee consists of no teachers
Total number of non-teachers in the population = 6 + 4=10
Therefore,
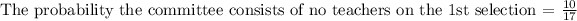
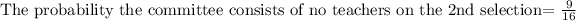
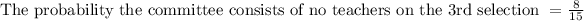
Therefore,