The Solution:
Given the pair of sequences below:
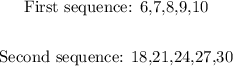
We are asked to write a statement that correctly describes the relationship between the two sequences.
The two sequences are both linear sequences. Their common differences are:
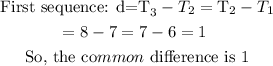
The general formula for the first sequence is
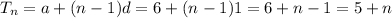
Similarly,
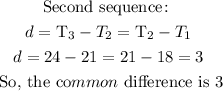
The general formula for the second sequence is
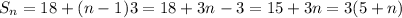
Thus, the relationship between the two sequences is:

Where
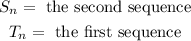
Therefore, the correct answer is:
