Question

Topic 8.2: Solving Using Linear/HELP RN!!!!!Area Scale Factor3. Examine the two similar shapes below. What is the linear scale factor? What is the area scalefactor? What is the area of the smaller shape?3a. Linear scale factor =3b. Area scale factor =Area =99 un.2=3c. Area of small shape =

Answer 1

Question 3:

- Let the dimension of a shape be x and the dimension of its enlarged or reduced image be y.

- The linear scale factor will be:

`sf_L=(y)/(x)`

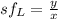
- If the area of the original shape is Ax and the Area of the enlarged or reduced image is Ay, then, the Area scale factor is:

`sf_A=(A_y)/(A_x)=(y^2)/(x^2)`

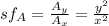
- We have been given the area of the big shape to be 99un² and the dimensions of the big and small shapes are 6 and 2 respectively.

- Based on the explanation given above, we can conclude that:

`\begin{gathered} \text{ If we choose }x\text{ to be 6, then }y\text{ will be 2. And if we choose }x\text{ to be 2, then }y\text{ will be 6} \\ \text{ So we can choose any one.} \\ \\ \text{ For this solution, we will use }x=6,y=2 \end{gathered}`

- Now, solve the question as follows:

`\begin{gathered} \text{ Linear Scale factor:} \\ sf_L=(y)/(x)=(2)/(6)=(1)/(3) \\ \\ \text{ Area Scale factor:} \\ sf_A=(y^2)/(x^2)=(2^2)/(6^2)=(1)/(9) \\ \\ \text{ Also, we know that:} \\ sf_A=(A_y)/(A_x)=(y^2)/(x^2) \\ \\ \text{ We already know that }(y^2)/(x^2)=(1)/(9) \\ \\ \therefore(A_y)/(A_x)=(1)/(9) \\ \\ A_x=99 \\ \\ (A_y)/(99)=(1)/(9) \\ \\ \therefore A_y=(99)/(9) \\ \\ A_y=11un^2 \end{gathered}`

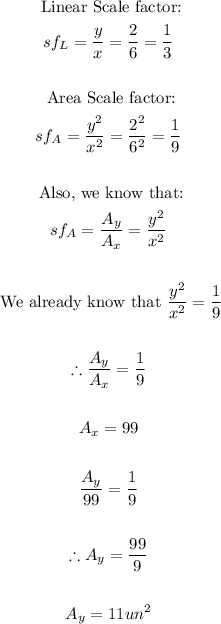
Final Answer

The answers are:

`\begin{gathered} \text{ Linear Scale Factor:} \\ (1)/(3) \\ \\ \text{ Area Scale Factor:} \\ (1)/(9) \\ \\ \text{ Area of smaller shape:} \\ 11un^2 \end{gathered}`