To find the positive intervals, we'll have:
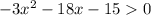
1. Divide both sides by -3:
(Remember that dividing or multiplying by a negative number turns the inequality around!)
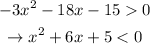
2. Factor the expression:
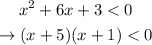
3. Identify the interval we're looking for:
Therefore, the function is positive in the interval:
[tex]\begin{gathered} -5