Question

How do you know if something is one solution,no solution, or infinite solutions?

Answer 1

A linear equation can have solutions in three forms: one solution, no solution, and infinite solutions.

ONE SOLUTION EQUATION:

These are equations that will give only one solution when solved, such that the variable is equal to a single answer.

If the graph is drawn, the linear equations all cross or intersect at one point in space.

An example of a one-solution equation is shown below:

`3x+5=2x-7`

Solving this equation, we have:

`\begin{gathered} 3x-2x=-7-5 \\ x=-12 \end{gathered}`

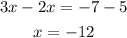
We can therefore see that it has only one solution, one value for x which is -12.

NO SOLUTION EQUATION:

In this case, the coefficients of the variables on both sides of the equation are the same. Simplifying the equation will give an expression that is not true.

Graphically, the system is inconsistent and the linear equations do not all cross or intersect.

Consider the equation below:

`2x+5=2x-7`

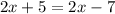
If we attempt to solve the equation by subtracting 2x from both sides, we have the solution below:

`\begin{gathered} 2x+5-2x=2x-7-2x \\ 5=-7 \end{gathered}`

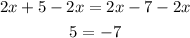
We can see that what we have left is not a valid statement, since 5 is not equal to -7:

`5\\eq-7`

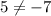
Thus, we can say that the equation has no solutions.

INFINITE SOLUTION EQUATION:

This follows the same format as the no solution equations. However, the final statement gotten from the simplification of the equation will give us a true statement instead.

Graphically, the linear equations are the same line in space and some variables are unconstrained.

Consider the equation below:

`2x+5=2x+5`

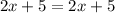
If we subtract 2x from both sides, we have:

`\begin{gathered} 2x+5-2x=2x+5-2x \\ 5=5 \end{gathered}`

Since the statement left is true, as 5 is equal to 5, then the equation has an infinite number of solutions.