Given :-
To Find :-
- The roots of the equation .
Solution :-
As we know that if the quadratic equation is in standard form which is ,

Then its roots are given by ,
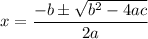
So on converting the equation in standard form ,

With respect to the standard form ,
Substitute in the Quadratic formula ,
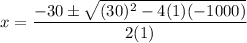
Simplify,
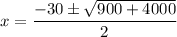
Add the numbers inside square root ,
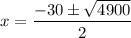
Divide each term in numerator by 2,
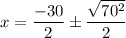
Simplify ,
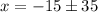
Separate the two solutions ,
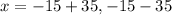
Simplify ,
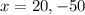
Hence the solution of the equation are 20 and -50 .
I hope this helps.