Question

Correctz is jointly proportional to x and y. If z = 115 when x = 8 and y = 3, find z when x = 5 and y = 2. (Round off your answer to the nearest hundredth.)

Answer 1

When we have a number that is jointly proportional to two other numebrs, the formula is:

`a=kcb`

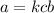
This means "a is jointly proportional to c and b with a factor of k"

Then, we need to find the factor k.

In this case z is jointly proportional to x² and y³

This is:

`z=kx^2y^3`

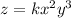
Then, we know that z = 115 when x = 8 and y = 3. We can write:

`115=k\cdot8^2\cdot3^3`

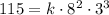
And solve:

`\begin{gathered} 115=k\cdot64\cdot27 \\ 115=k\cdot1728 \\ k=(115)/(1728) \end{gathered}`

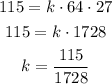
NOw we can use k to find the value of z when x = 5 and y = 2

`z=(115)/(1728)\cdot5^2\cdot2^3=(115)/(1728)\cdot25\cdot8=(2875)/(216)\approx13.31`

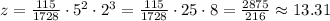
To the nearest hundreth, the value of z when x = 5 and y = 2 is 13.31