Step 1
Given
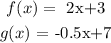
Required: To find where the graph of both functions intersect. In other words the find the value of x and hence f(x) and g(x).
Step 2
Solve both equations simultaneously.

Subtract equation 2 from 1
Hence,
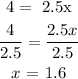
Step 3
Check
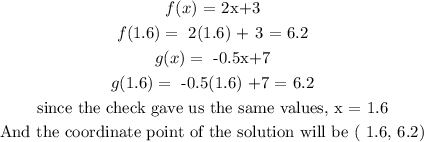
Hence the graph intersects at the point where x = 1.6 and y =6.2. Remember y = f(x) and g(x)