To find the time it takes the object to reach the maximum height we need to remember that this happens in the axis of symmetry of the parabola described by the function:
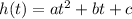
The axis of symmetry is given as:
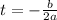
in this case we have that a=-16 and b=64, then we have:
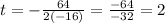
Therefore it takes 2 seconds to the object to reach its maximum height.
Now, to find the maximum height we plug this value of t in the equation, then we have:
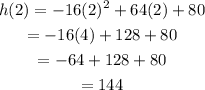
therefore the maximum height is 144 ft.