To help us solve this problem let's plot the points given in the table:
From the graph we notice that this the position can be modeled by a sine function, we also notice that the period of this function is 8. We know that a sine function can be modeled by:
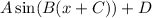
where A is the amplitude, C is the horizontal shift, D is the vertical shift and
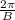
is the period.
From the graph we have we notice that we don't have any horizontal or vertical shift, then C=0 and D=0. We also notice that the amplitude is 15, then A=15. Finally, as we said, the period is 8, then:
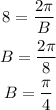
Plugging these values in the sine function we have:
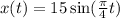
If we graph this function along the points on the table we get the following graph:
We notice that we don't get an exact fit but we get a close one.
Now, that we have a function that describes the position we can find the velocity by taking the derivative:
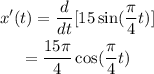
Therefore, the velocity is:
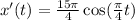
Once we have the expression for the velocity we can find values for the times we need, they are shown in the table below:
From the table we have that:
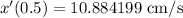
And that:
• The earliest time when the velocity is zero is 2 s.
,
• The second time when the velocity is zero is 6 s.
,
• The minimum velocity happens at 4 s.
,
• The minimum velocity is -11.780972 cm/s