Question

An ordinary (Pair) die is a cube with the numbers 1 through 6 on the sides (represented by painted spots). Imagine that such a die is rolled twice in successionand that the face values of the two rolls are added together. This sum is recorded as the outcome of a single trial of andereCompute the probability of each of the following svents.Event A: The sum is greater than 7.Event B: The sum is divisible by 3 or 6 (or both).Write your answers as fractions

Answer 1

`P(A)=(5)/(12),P(B)=(1)/(3)`

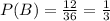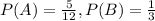
1) We are going to tackle this question starting with the total outcomes of dice rolled twice in succession.

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

So we can see that there are 36 possibilities.

2) Let's examine the events.

a) P (>7)

Let's bold the combinations of outcomes whose sum is greater than 7

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

So, we can see that there are 15 favorable outcomes.

Now, we can find the Probability of rolling the dice twice and get a sum greater than 7:

`P(A)=(15)/(36)=(5)/(12)`

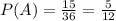
b) Now, for the other event: The sum is divisible by 3 or 6, or both:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

Hence, the favorable outcomes are: 12

So now, let's find the probability of getting a sum that way:

`P(B)=(12)/(36)=(1)/(3)`