Question

Use substitution to find the solution to the linear/quadratic system. y - 2x^2 = 4x + 1 y = 14x - 7 Blank 1: (___7) Blank 2: (___49) Blank # 1:Blank # 2:

Answer 1

The given system is

`\mleft\{\begin{aligned}y-2x^2=4x+1 \\ y=14x-7\end{aligned}\mright.`

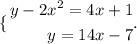
Let's replace the second equation with the first one.

`14x-7-2x^2=4x+1`

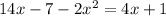
Now, we solve the quadratic equation.

`\begin{gathered} 14x-7-2x^2-4x-1=0 \\ -2x^2+10x-8=0 \\ -2(x^2-5x+4)=0 \\ x^2-5x+4=0 \end{gathered}`

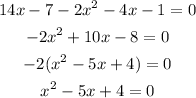
Then, we have to find two numbers whose product is 4 and whose sum is 5. Those numbers are 4 and 1.

`\begin{gathered} (x-4)(x-1)=0 \\ x_1=4 \\ x_2=1 \end{gathered}`

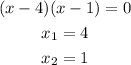
We use these values to find y.

`\begin{gathered} y_1=14\cdot4-7=49 \\ y_2=14\cdot1-7=7 \end{gathered}`

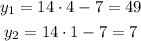
Hence, the solutions to the given system are (4,49) and (1,7).