Question

Find the equation of the linear function represented by the table below inslope-intercept form.xy1-3 -723-114-15

Answer 1

To find the linear equation, we use two points from the table (1, -3) and (3, -11). First, we have to find the slope with the following formula.

`m=(y_2-y_1)/(x_2-x_1)`

Where,

`\begin{gathered} x_1=1 \\ x_2=3 \\ y_1=-3 \\ y_2=-11 \end{gathered}`

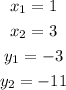
Let's those coordinates to find the slope.

`\begin{gathered} m=\frac{-11-(-3)_{}}{3-1}=(-11+3)/(2)=(-8)/(2)=-4\to m=-4 \\ \end{gathered}`

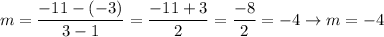
The slope is -4.

Now, we use the point-slope formula to find the equation.

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-3)=-4(x-1) \\ y+3=-4x+4 \end{gathered}`

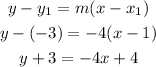
Now, we solve for y to express it in slope-intercept form.

`\begin{gathered} y+3=-4x+4 \\ y=-4x+4-3 \\ y=-4x+1 \end{gathered}`

Therefore, the equation in slope-intercept form is y = -4x+1.