Question

I I need help solving problem number 8 please :)

Answer 1

(8, -1)

Step-by-step explanation:

Given the below system of equations;

`\begin{gathered} y^2+x^2=65\ldots\ldots\ldots\text{.Equation 1} \\ y+x=7\ldots\ldots\ldots\ldots\text{.Equation 2} \end{gathered}`

Let's go ahead and test each of the given solutions and see which of them is the correct one;

For (8, -1), we have x = 8 and y = -1;

Substituting the above values in Equation 1, we have;

`\begin{gathered} (-1)^2+(8)^2=65 \\ 1+64=65 \\ 65=65 \end{gathered}`

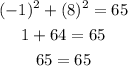
Substituting the values into Equation 2;

`\begin{gathered} (-1)+8=7 \\ -1+8=7 \\ 7=7 \end{gathered}`

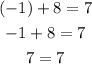
We can see that (8, -1) is a solution to the given system of equations