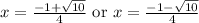Question

3(4x+1)^2-5=25 using square root property

Answer 1

`x=(-1+√(10))/(4)\text{ or }x=(-1-√(10))/(4)`

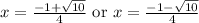
Step-by-step explanation:

Given the equation:

`3\left(4x+1\right)^2-5=25`

To solve an equation using the square root property, begin by isolating the term that contains the square.

`\begin{gathered} 3(4x+1)^(2)-5=25 \\ \text{ Add 5 to both sides of the equation} \\ 3(4x+1)^2-5+5=25+5 \\ 3(4x+1)^2=30 \\ \text{ Divide both sides by 3} \\ (3(4x+1)^2)/(3)=(30)/(3) \\ (4x+1)^2=10 \end{gathered}`

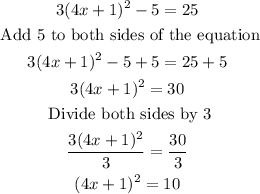
After isolating the variable that contains the square, take the square root of both sides and solve for the variable.

`\begin{gathered} √((4x+1)^2)=\pm√(10) \\ 4x+1=\pm√(10) \\ \text{ Subtract 1 from both sides} \\ 4x=-1\pm√(10) \\ \text{ Divide both sides by 4} \\ (4x)/(4)=(-1\pm√(10))/(4) \\ x=(-1\pm√(10))/(4) \end{gathered}`

Therefore, the solutions to the equation are:

`x=(-1+√(10))/(4)\text{ or }x=(-1-√(10))/(4)`