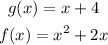This operation is equivalent to:
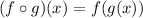
It is like a function inside a function. So, we can look for parts in h(x) that are common and call that the function inside.
As we can see, h(x) have terms with x + 4, so if we call:
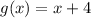
We can see that h(x) becomes:
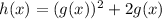
And if we substitute g(x) by x, we will get the expression of the ouside function f(x):
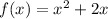
This way, we have:
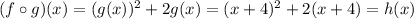
So, the functions are: