Question

Which function has the greatest average rate of change on the interval [1,5]

Answer 1

Step-by-step explanation:

Given: interval [1,5]

Based on the given functions, we start by computing the function values at each endpoint of the interval.

For:

`\begin{gathered} y=4x^2 \\ f(1)=4(1)^2 \\ =4 \\ f(5)=4(5)^2 \\ =100 \\ \end{gathered}`

Now we compute the average rate of change.

`\begin{gathered} \text{Average rate of change = }(f(5)-f(1))/(5-1) \\ =(100-4)/(5-1) \\ \text{Calculate} \\ =24 \end{gathered}`

For:

`\begin{gathered} y=4x^3 \\ f(1)=4(1)^3 \\ =4 \\ f(5)=4(5)^3 \\ =500 \end{gathered}`
`\begin{gathered} \text{Average rate of change = }(f(5)-f(1))/(5-1) \\ =(500-4)/(5-1) \\ =124 \end{gathered}`

For:

`\begin{gathered} y=4^x \\ f(1)=4^1 \\ =4 \\ f(5)=4^5 \\ =1024 \end{gathered}`
`\begin{gathered} \text{Average rate of change = }(f(5)-f(1))/(5-1) \\ =(1024-4)/(5-1) \\ =255 \end{gathered}`

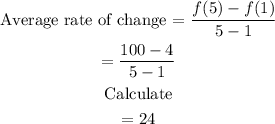
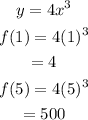
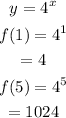
For:

`\begin{gathered} y=4\sqrt[]{x} \\ f(1)=4\sqrt[]{1} \\ =4 \\ f(5)\text{ = 4}\sqrt[]{5} \\ \end{gathered}`
`\begin{gathered} \text{Average rate of change = }(f(5)-f(1))/(5-1) \\ =\frac{(4\sqrt[]{5\text{ }})\text{ -4}}{5-1}\text{ } \\ =1.24 \end{gathered}`

Therefore, the function that has the greatest average rate is

`y=4^x`