Given:
The triangle having two similar angles.
This is the isosceles traingle.
Draw the altitude to the given traingle,
D divides the side BC into two equal side having length,
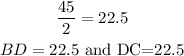
Now, use the tan ratio for right triangle ABD,
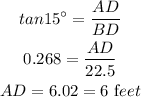
Using the pythagorean theorem,
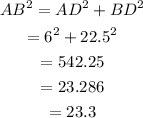
The length of the sloping side of the roof is 23.3 feet.