Question

a teacher bought 4 folders and 9 books for $33.75. on another day, she bought 3 folders and 12 books at the same prices for $34.50. how much did she pay for each folder and each book?

Answer 1

The teacher made two different purchases:

First purchase:

4 folders and 9 books for $33.75

Second purchase

3 folders and 12 books for $34.50

Let "f" represent the cost of each folder and "b" represent the cost of each book. You can express the total cost of each purchase as equations:

`\begin{gathered} 1)4f+9b=33.75 \\ 2)3f+12b=34.50 \end{gathered}`

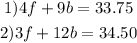
Now we have established a system of equations, to solve it, the first step is to write one of the equations in terms of one of the variables.

For example, I will write the first equation in terms if "f"

`\begin{gathered} 4f+9b=33.75 \\ 4f=33.75-9b \\ (4f)/(4)=(33.75-9b)/(4) \\ f=(135)/(16)-(9)/(4)b \end{gathered}`

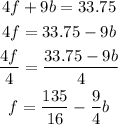
The second step is to replace the expression obtained for "f" in the second equation:

`\begin{gathered} 3f+12b=34.50 \\ 3((135)/(16)-(9)/(4)b)+12b=34.50 \end{gathered}`

Distribute the multiplication on the parentheses term

`\begin{gathered} 3\cdot(135)/(16)-3\cdot(9)/(4)b+12b=34.50 \\ (405)/(16)-(27)/(4)b+12b=34.50 \\ (405)/(16)+(21)/(4)b=34.50 \end{gathered}`

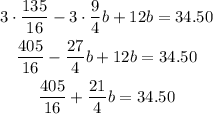
Pass the number to the right side of the equal sign by applying the opposite operation to both sides of it

`\begin{gathered} (405)/(16)-(405)/(16)+(21)/(4)b=34.50-(405)/(16) \\ (21)/(4)b=(147)/(16) \end{gathered}`

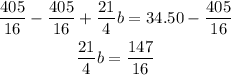
Now divide b by 21/4 to cancel the multiplication and to keep the equality valid, you have to divide both sides of the expression, so divide 147/16 by 21/4 too, or multiply them by its reciprocal fraction, 4/21, is the same.

`\begin{gathered} ((21)/(4)\cdot(4)/(21))b=((4)/(21)\cdot(147)/(16)) \\ b=(7)/(4)\approx1.75 \end{gathered}`

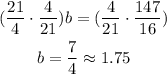
Each book costs $1.75

Now that we have determined how much does each book cost, we can determine the cost of each folder by replacing the value of "b" in the expression obtained for "f"

`\begin{gathered} f=(135)/(16)-(9)/(4)b \\ f=(135)/(16)-(9)/(4)\cdot(7)/(4) \\ f=(9)/(2)\approx4.5 \end{gathered}`

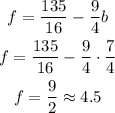
Each folder costs $4.50