In the given expression
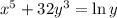
To differentiate it with respect to it, we will writ y' for every term of y
The differentiation of

The differentiation of
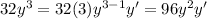
The differentiation of
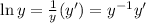
Now let us write all of them in one line
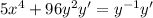
Put the terms of y' on one side and the other term on the other side
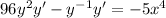
Take y' as a common factor
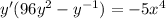
Divide both sides by the bracket

Since the given point is (-2, 1), then
x = -2 and y = 1
Substitute them to find y'

The value of y' is -16/19