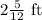Question

A rectangular calendar is hanging on a wall. The diagram below shows several dimensions of the wall and the calendar.Based on the diagram, determine the distance that the top edge of the calendar is from the ceiling, and explain your reasoning.

Answer 1

We want to find the distance that the top edge of the calendar is from the ceiling.

The diagram below will help us

From the diagram above x is the distance we want to find

We can see that the entire wall is 9 ft long,

Distance from the foot of the calender to the floor is 5 1/4 ft and

Halve of the calendar is 2/3 ft

So the whole calendar is

`\begin{gathered} 2*(2)/(3) \\ =(4)/(3)\text{ ft } \end{gathered}`

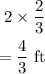
So, to find x, we will add length of the calendar which is 4/3 ft to distance from the foot of the calender to the floor which is 5 1/4 ft and subtract this from height of the wall which is 9 ft

We have

`\begin{gathered} 9-((4)/(3)+5(1)/(4)) \\ 9-((4)/(3)+(21)/(4)) \\ 9-((16+63)/(12)) \\ 9-(79)/(12) \\ =(108-79)/(12) \\ =(29)/(12) \\ =2(5)/(12) \end{gathered}`

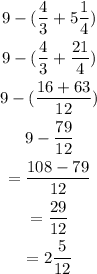
Hence the answer is

`2(5)/(12)\text{ ft}`