Question

Write the curve equation associated to those parametric equations.x(θ) = 3 cos θy(θ) = 6 sin θ

Answer 1

We want to rewrite the following parametric equations

`\begin{gathered} \begin{cases}x={3\cos\theta} \\ y={6\sin\theta}\end{cases} \\ (\pi)/(2)<\theta<(3\pi)/(2) \end{gathered}`

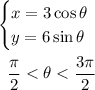
as one equation. Using the following property

`\sin^2\theta+\cos^2\theta=1`

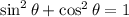
We can eliminate the parameter theta adding the square of the coordinates

`\begin{gathered} \sin^2\theta+\cos^2\theta=1 \\ 6^2(\sin^2\theta+\cos^2\theta)=6^2 \\ 6^2\sin^2\theta+6^2\cos^2\theta=6^2 \\ (6\sin\theta)^2+(6\cos\theta)^2=6^2 \\ (6\sin\theta)^2+(2\cdot3\cos\theta)^2=6^2 \\ (y)^2+(2x)^2=6^2 \\ y^2+4x^2=36 \\ (x^2)/(9)+(y^2)/(36)=1 \end{gathered}`

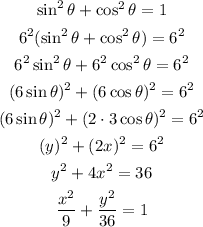
And this is the standard equation of an ellipse

`(x^(2))/(9)+(y^(2))/(36)=1`

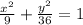
The constrain

`(\pi)/(2)<\theta<(3\pi)/(2)\implies x<0`

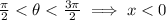
tells us that x can only assume negative values, therefore, the graph is only the left side of the ellipse.