Question

Yea I do it all right I just got the one

Answer 1

`v_0=20.7(m)/(s)`

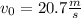
Step-by-step explanation:

We are given the equation for the height:

`h(t)=10+v_0t-4.9t^2`

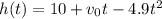
If we differentiate this equation, we get the equation of the velocity:

`h^(\prime)(t)=v(t)=v_0-9.8t`

The problem tells us that the object hits the ground at a velocity of -25m/s. We can write this:

`-25=v_0-9.8t_0`

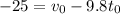
Where t0 is the time when the object hits the ground, and the velocity is -25m/s

Now, we can solve for v0:

`v_0=9.8t_0-25`

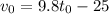
And if we use this in the height h(t) equation, we can find the value of t0. At t0, the height is 0. Thus:

`0=10+(9.8t_0-25)t_0-4.9t_0^2`

And solve:

`\begin{gathered} 0=10+9.8t_o^2-4.9t_0^2-25t_0 \\ 0=10-25t_0+4.9t_0^2 \end{gathered}`

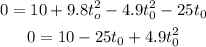
Next, we can use the quadratic formula to solve this:

`\begin{gathered} t_(\pm)=(-(-25)\pm√((-25)^2-4\cdot4.9\cdot10))/(2\cdot4.9)=(25\pm√(625-196))/(9.8)=(25\pm√(429))/(9.8)=(25\pm20.71231)/(9.8) \\ . \\ t_+=(25+20.71231)/(9.8)=4.664521seconds \\ . \\ t_-=(25-20.71231)/(9.8)=0.43751seconds \end{gathered}`

Let's see which of the two solutions is the time we are looking for.

Let's go back to our solution for v0:

`v_0=9.8t_0-25`

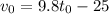
If we use t0 = 0.43751 s:

`v_0=9.8\cdot0.46751-25=-20.7123m/s`

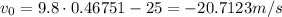
This means that the initial velocity is negative, thus the object goes downwards. But, the problem tells us that initially the object is thrown upwards.

The correct value of t0 = 4.66 seconds

Now we can find v0:

`v_0=9.8\cdot4.664521-25=20.712`

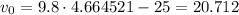
Thus, v0 = 20.7 m/s