SOLUTION.
The area of the entire region will be to find the area of the isosceles triangle and the semi-circle.
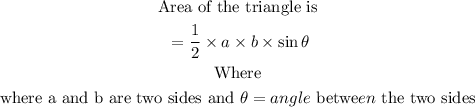
Then
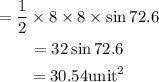
The area of the isosceles triangle is 30.354 square units
We need to obtain the diameter of the semi-circle using the cosine rule
We need to obtain the value of x,
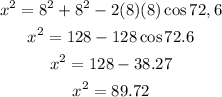
Take square root of both sides, we have
![x=\sqrt[]{89.72}=9.74](https://img.qammunity.org/2023/formulas/mathematics/high-school/v1t3dwv36h8jhlet8l3pujrxx8pyi8ahfj.png)
Hence, the diameter is 9.74
Then the radius will be
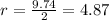
The area of the semi-circle is
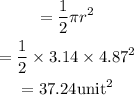
The area of the semi circle is 37.42 square units
Therefore the area of the region will be

Thus
The area of the region is 67.96 units²