Question

What are the intersection points of the parabola given by the equation y=x^2 - 9 and the line given by the equation y = x - 3?

Answer 1

Since we want the points where both the parabola and the line have in common (i.e., they intersect), then we have the following:

`\begin{gathered} y=x^2-9 \\ y=x-3 \\ \Rightarrow x^2-9=x-3 \end{gathered}`

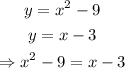
Now we solve for x to find the first two values of the points that we are looking for:

`\begin{gathered} x^2-9=x-3 \\ \Rightarrow x^2-9-x+3=0 \\ \Rightarrow x^2-x-6=0 \\ \Rightarrow(x-3)\cdot(x+2)=0 \\ x_1=3 \\ x_2=-2_{} \end{gathered}`

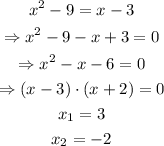
Now we use these values of x to find other pair of values for y:

`\begin{gathered} y=x-3 \\ x_1=3 \\ \Rightarrow y_1=3-3=0 \\ \Rightarrow(x_1,y_1)=(3,0) \\ x_2=-2 \\ \Rightarrow y_2=-2-3=-5 \\ \Rightarrow(x_2,y_2)=(-2,-5) \end{gathered}`

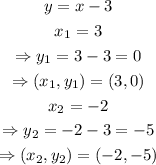
Therefore, the intersection points are (3,0) and (-2,-5)