Question

Express the trig ratios as fractions in simplest form.Drop down menu: (a) are equal (b) are not equal

Answer 1

`\begin{gathered} \sin O=(34)/(35) \\ \\ \cos N=(34)/(35) \\ \\ \text{ They are equal.} \end{gathered}`

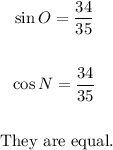
Step-by-step explanation

We want to express the trigonometric ratios as fractions in the simplest terms.

The trigonometric ratios SOHCAHTOA for right triangles for sine and cosine are:

`\begin{gathered} \sin\theta=(opposite)/(hypotenuse) \\ \\ \cos\theta=(adjacent)/(hypotenuse) \end{gathered}`

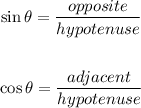
Therefore, for the given triangle, we have that:

`\begin{gathered} \sin O=(34)/(35) \\ \\ \cos N=(34)/(35) \end{gathered}`

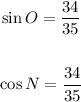
As we see from the equations above, the sine of O and the cosine of N are equal.