Answer:
Let the first number be
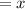
Let the second number be
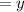
The sum of two numbers is 83 can be represented below as

The difference of the 2 numbers is 13 can be represented below as

Step 1:
From equation (1) make x the subject of the formula to to give equation (3)
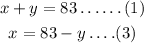
Step 2:
Substitute equation (3) in equation (2)
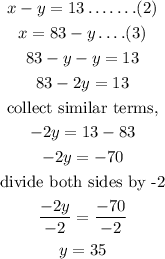
Step 3:
Substitute y= 35 in equation (3)
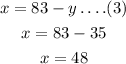
Hence,
The product of the two numbers will be calculated as
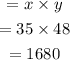
Hence,
The final answer is = 1680
OPTION D is the final answer