ANSWER
38.34 m/s
Step-by-step explanation
Given:
• The mass of the coaster, m = 839 kg
,
• The initial height of the coaster, h = 75 m
,
• The acceleration due to gravity, g = 9.8 m/s²
Find:
• The final velocity of the roller coaster at the bottom of the hill, v.
The roller coaster starts from rest, so at the top of the hill, it only has gravitational potential energy and no kinetic energy. Then, at the bottom of the hill, the roller coaster is in motion, to it has kinetic energy, and, because the difference of height with the reference - which is the bottom of the hill, is zero, it has no potential energy,
By the work-energy theorem, we have the equation,
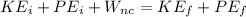
As explained above, the initial kinetic energy is 0 and the final potential energy is also 0. If we assume that there is no friction, air resistance, or other external forces, then the work done by non-conservative forces is also 0,
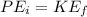
Replace each kind of energy with the expression to obtain them,
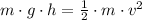
The mass cancels out,
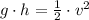
Solving for v,
![v=\sqrt[]{2\cdot g\cdot h}](https://img.qammunity.org/2023/formulas/physics/college/pkcssarjde3ws0ouygjjpckkhqb4q37t0g.png)
Replace with the known values and solve,
![v=\sqrt[]{2\cdot9.8m/s^2\cdot75m}=\sqrt[]{1470m^2/s^2}\approx38.34m/s](https://img.qammunity.org/2023/formulas/physics/college/d0guss23tyr0575b79e98q30rhki1qdghc.png)
Hence, the velocity of the roller coaster at the bottom of the hill is 38.34 m/s, rounded to the nearest hundredth.