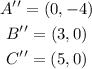Given the graph of f(x):
Where the points A, B, and C have the coordinates:
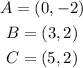
Now, the transformation -f(x) is just a reflection about the x-axis. This is equivalent to a change of sign on the y-coordinate. The new points A', B', and C' are:
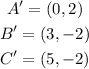
And the graph looks like this:
Now, for the f(x) - 2 transformation, we see that this is just a shift of 2 units down. Then:
Where: