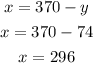Assuming these are volume percentages and the volumes don't change when you mix them, we can calculate this using a system of equations.
But first we need to identify each equation and variable.
let x be the volume of 7% vinegar used and y be the volume of 12% vinegar used.
The total volume is the sum of those and it must be equal to 370 mL, so:
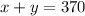
The amount of vinegar in the x volume of 7% vinegar can be calculated by multiplying x by the 7%, that is, by 0.07:
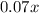
Similarly, the amount of vinegar in y is:
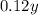
So, the total amount of vinegar after the mixture is:
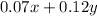
Since the percentage of the final mixture is 8%, the amount after the mixture can also be calculated by taking 8% of the final volume of 370mL, that is:
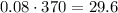
The two ways of calculating the amount of vinegar in the mixture must be the same, so we have got our second equation:
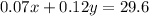
So, the system of equations is:
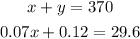
We can solve this by substitution:
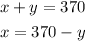
Thus:
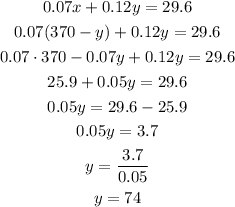
And, going back to the first equation: