Volume of the top of the prism: 460 cm^3
Volume of the bottom of the prism: 1 768 cm^3
Total volume of the figure: 2 228 cm^3
Step-by-step explanation:
Volume of the top of the prism:
. Since it is a prism from trapezoid
. . Volume = Area of the trapezium base * heights between trapezium ends

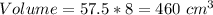
Volume of the bottom prism:
. Since the price has a rectangular base:
Volume = Area of one base * height between reactangular bases
Area of one base :

Volume:
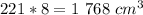
Total volume of the figure:
Volume of the top + Volume of the bottom = Total volume
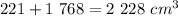
NB:
To find any volume of a given prism, start with finding the area of one base, then multiply that area by the height (in other words the sides that link the two bases)