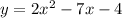In general, a quadratic equation can be written in terms of its solutions:
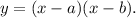
Now, notice that:
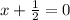
when x= -1/2, and it is equivalent to:
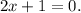
Therefore, you can write the quadratic equation as:
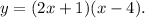
Computing the above multiplication, you get:
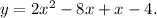
Simplifying the above equation you get:
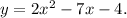
Answer: